04-21-2015, 11:46 PM
(This post was last modified: 04-22-2015, 06:25 PM by brandonio21.)
Hello,
I recently had a final exam on which my teacher asked to write a method for Knuth numbers recursion. I got a stack overflow on my implementation, and I am new on Java, so I am not sure what happened, it might be that I had the wrong formula for Knuth numbers? I would love some feedback.
Here is the question, and my code
Knuth numbers are given by the recursive formula Kn+1 = 1 + min (2 * Ka, 3 * Kb) where a is the smallest integer larger than n/2.0 and b is the smallest integer larger than n/3.0. The use of doubles in the denominator is necessary to ensure that integer division is not used.
For example, if n is 7, then a equals 4 and b equals 3 and thus K8 = 1 + min (2* K4, 3 * K3).
If n is 8, then a equals 5 while b remains 3 and thus K9 = 1 + min (2 * K5, 3 * K3).
If n is 9, then a remains 5 while b equals 4 and thus K10 = 1 + min(2 * K5, 3 * K3).
Mathematically, “the smallest integer larger than x†is the “ceiling†function. If n is an int, then n / 2 is calculated using integer division, discarding the remainder; but you want the division to give you a double. Thus you need code that looks like this:
int a = Math.ceil(n / 2.0);
int b = Math.ceil(n / 3.0);
Since the equation defining Knuth numbers is a recursive one, we must have a base case; let’s assume that K0 = 1.
Create and test a class called KnuthNumbers (in a project also called KnuthNumbers) which includes a static method to compute Knuth numbers.
my code:
TEST:
I recently had a final exam on which my teacher asked to write a method for Knuth numbers recursion. I got a stack overflow on my implementation, and I am new on Java, so I am not sure what happened, it might be that I had the wrong formula for Knuth numbers? I would love some feedback.
Here is the question, and my code
Knuth numbers are given by the recursive formula Kn+1 = 1 + min (2 * Ka, 3 * Kb) where a is the smallest integer larger than n/2.0 and b is the smallest integer larger than n/3.0. The use of doubles in the denominator is necessary to ensure that integer division is not used.
For example, if n is 7, then a equals 4 and b equals 3 and thus K8 = 1 + min (2* K4, 3 * K3).
If n is 8, then a equals 5 while b remains 3 and thus K9 = 1 + min (2 * K5, 3 * K3).
If n is 9, then a remains 5 while b equals 4 and thus K10 = 1 + min(2 * K5, 3 * K3).
Mathematically, “the smallest integer larger than x†is the “ceiling†function. If n is an int, then n / 2 is calculated using integer division, discarding the remainder; but you want the division to give you a double. Thus you need code that looks like this:
int a = Math.ceil(n / 2.0);
int b = Math.ceil(n / 3.0);
Since the equation defining Knuth numbers is a recursive one, we must have a base case; let’s assume that K0 = 1.
Create and test a class called KnuthNumbers (in a project also called KnuthNumbers) which includes a static method to compute Knuth numbers.
my code:
Code:
public class KnuthNumbers
{
  /**
  * Recursive Knuth Numbers 1, 3, 3, 4, 7, 7, 7, 9, 9, 10, 13, ... Â
  */
  public static int knuthNumber(final double n)
  throws DataFormatException{
    double a = Math.ceil(n / 2.0);
    double b = Math.ceil(n / 3.0);
    // bad input
    if (n < 1)
      throw new DataFormatException("n cannot be less then 1");
    if (n > 12)
      throw new DataFormatException("n is too large. Max is 12");
    //base case
    if (n == 1)
      return 1;
    //recursion
    return knuthNumber(a + b);
  }
}TEST:
Code:
public class KnuthNumbersTest
{
 Â
  @Test
  public void testKnuthNumber(){
    long startTime = 0;
    long endTime = 0;
    double result = 0;
    try {
      assertEquals(-1, KnuthNumbers.knuthNumber(-3));
      fail("number should not be negative");
    }
    catch (DataFormatException e){
      assertEquals("n cannot be less then 1", e.getMessage());
    }
    catch (Exception e) {
      fail("Unexpected exception: " + e.toString());
    }
    try {
      assertEquals(0, KnuthNumbers.knuthNumber(0));
      fail("number should not be zero");
    }
    catch (DataFormatException e){
      assertEquals("n cannot be less then 1", e.getMessage());
    }
    catch (Exception e) {
      fail("Unexpected exception: " + e.toString());
    }
    try {
      assertEquals(1, KnuthNumbers.knuthNumber(1.0));
      assertEquals(9, KnuthNumbers.knuthNumber(5.4));
      assertEquals(13, KnuthNumbers.knuthNumber(7.6));
    }
    catch (Exception e) {
      fail ("Unexpected exception: " + e.toString());
    }
  }
}
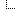


![[Image: NumberedEquation1.gif]](http://mathworld.wolfram.com/images/equations/KnuthNumber/NumberedEquation1.gif)